Since this post veers into very inside baseball territory, let’s start with how we got here.
Have you ever had that book that you had to take with you everywhere? It could be the latest exciting story you were reading, or a really handy reference guide, or something with deep sentimental value. Maybe this book has been a passenger in your car; you take it out to lunch even though you know you’re not going to read it while you eat because you might get sauce on the pages. You just want to pick this book up and hold it, flip through the pages, feel the weight of it as you toss it from hand to hand. Maybe you even… smell the pages. That sort of book.
My latest book of this type is “A Perspective in Theoretical Computer Science: Commemorative Volume for Gift Siromoney“:

I know, it’s cliché. Everyone loves this book and has a copy next to their nightstand.
No? Just me, then? Okay.
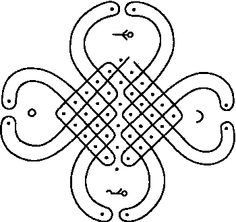
Why this book is important is that it is the end of a long trail of looking through references in papers, from a stray mention of Kolam patterns in a L-System book by Przemyslaw Prusinkiewicz to the work of Darrah Chavey, Paulus Gerdes, Marcia Ascher and countless others. This book has some of the best grounding in the computer science behind drawing curved line patterns using context-free and array grammars, and contains images from work in the field. It is perfect because it is obscure and exactly the right book at the right time, even though it was written almost 30 years ago.
Which brings me to mathematical notation.
As a fledging programmer one of the first things they teach you is to use meaningful variable names. A variable is an object that holds a value. So if I’m counting oranges, I might have a variable called numOranges. What I wouldn’t have is a variable called ‘o’. ‘o’ could be anything: orangutans, oscilloscopes, Timothy Olyphants, etc.
Math on the other hand tends to use one letter symbols all the time. You’d think this was okay, because the symbols only ever have one meaning. A ‘+’ symbol is a plus symbol. ‘π’ is pi the number.
Except when π is an iteration symbol, or a time stage symbol. And ‘x’ means multiplication, until you graduate to Algebra where a dot is now multiply and x is a variable. And ‘+’ could mean turn right if we’re talking L-systems.
Math papers in general make an assumption about mathematicians that isn’t always correct. It assumes they can write in a way that can be understood. They understand their field technically, but not in common language, or even readable technical language. Now I’m not picking on the Siromoney book too much. The text is very readable. Some of the paper’s problems come from problems in reproduction. Older books like this one had papers submitted physically and then photocopied into a full book. This was done a typewriter or an early word-processor (courier font is kind of a tip off that we’re looking at a typewriter), so some subscripts and superscripts are incorrect, and some symbols have to be hand-drawn after the paper is typed.
The bigger offenders are the ones who use a symbol without any explanation. I remember after staring at it for a few seconds that ∪ means union, but it might be nice to have some handy definitions at the back or in the text. Defining your terms is often a necessary part of making any proof, or explaining any new concept. It never hurts to make sure your audience is on the same page you are. Especially if you plan to have terms mean something other than their common meaning, like ∪ meaning recursive level, or some such.
For a while now, my goal with this new book has been to take complicated concepts and explain them in ways that make sense to everyone. These papers often do the opposite, take something simple and explain it in a complicated way. Fractals actually aren’t that hard to understand. More and more after reading these papers it feels like I’m translating from some arcane and obscure language, with symbols that change in meaning from one place to another.
It’s confusing, and it doesn’t have to be this way. We can be rigorous AND we can be clear. If you can explain a concept to a 6th grader, then you really understand it.