Sierpinski Triangle
Our first fractal is the Sierpinski Gasket, first described nearly 100 years ago in 1915, though it has appeared in mosaics as early as the 13th century, and is also one of the first fractals I encountered. The Sierpinski triangle is one of my favorites because it crops up in a number of different places, from the top levels of Pascal’s triangle to the Chaos Game I’ll describe in the going deeper section.
Constructing the triangle is fairly straightforward:
Step One: Draw a triangle (typically equilateral).
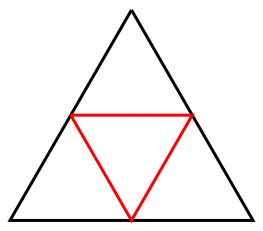
Step Two: Draw a point in the middle of each of the three sides of the triangle, and then connect those points to form a new triangle.
Now we have four smaller triangles, one in the middle and three in the corners. The triangle in the middle is pointing down, whereas the other three triangles are pointing up.
Step Three: Repeat Step Two for the outer three triangles, drawing a point in the middle of each of the sides and connecting the points to form a new triangle.
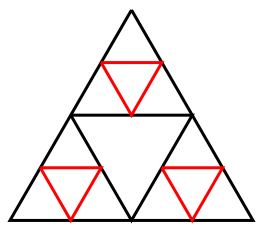
Each time we repeat step 2 is called an iteration, or how many times we’ve repeated the same operation. We now have a big triangle in the middle pointing down, and 3 smaller ones pointing down. If we were to stop here we’d color in each of the triangles pointing up black, and leave the triangles pointing down white. If we continue to repeat step 2, however, we would draw a point in the middle of each side of the 9 triangles pointing up and connect those points to form new triangles, repeating the process for each of the newly created triangles that are pointing up.
Here’s what we’d get after 5 iterations:
The above drawing took about 2 hours to complete and contains 243 black triangles. As you can see, even after only a few iterations, a very complex image starts to appear.
Going Deeper (The Chaos Game)
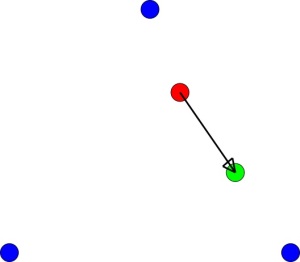
Let’s play a new game. First we draw the three vertices of a triangle and pick a random point somewhere inside it:
Roll a six-sided die. If you roll a 1 or a 2, go toward the vertex at the bottom left. If you roll a 3 or a 4, go toward the vertex on the bottom right, and if you roll a 5 or a 6, go toward the vertex at the top.
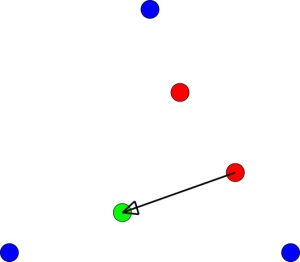
In the example below we rolled a 3.
Each roll of the die we move half the distance from where we are toward our selected vertex and draw a new point. We then repeat the process from our new point.
Let’s say we now roll a 1.
If we keep playing this game a familiar shape starts to emerge.
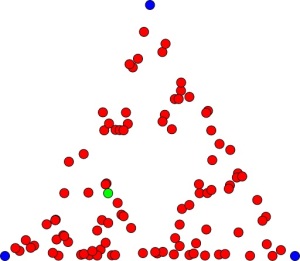
Here’s what we’d see after 100 rolls:
And after 50,000 (with the help of a computer).
There’s that gasket again!
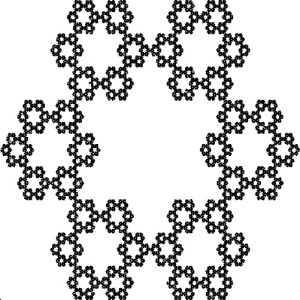
We can change the number of vertices and the amount of distance we move toward them to create a whole array of new shapes. Below we’ve made a Sierpinski Hexagon by choosing six vertices, and moving 2/3 the distance toward whichever vertex we roll.
Hidden in the center of this picture is our next fractal, the Koch Snowflake!
Bonus Question: If we continued iterating a Sierpinski triangle to infinity, what would the area of the black triangles be?
Want some fractals you can color? You might like my new Adult Coloring Book: Fractals.















Very cool, Ben! I knew the basic construction for the Triangle, but the Chaos Game, the Hexagon, and the Koch Snowflake being inside the Hexagon, were all new. Good stuff.
I’m guessing the area of the black triangles approaches zero as the iterations go to infinity. Any random point inside the big triangle would eventually get a sub-triangle drawn around it…right?
Yes, the area at infinite iterations is 0. The remaining area after each iteration is 3/4 of the previous area. When this is put in an infinite series the result is 0.
Pingback: Fractals You Can Draw (The Dragon Curve or The Jurassic Fractal) | Ben Trube
Pingback: Bonus Friday Post (Chaos Ensues) | Ben Trube
Pingback: The Very Inspiring Blogger Award! « M.S. Fowle
Pingback: Secret Non-Fiction Project Revealed! Surprise To All! | [BTW] : Ben Trube, Writer
Pingback: Blog Updates | [BTW] : Ben Trube, Writer
Pingback: Fractal Friday (Or Sierpinski Saturday) | [BTW] : Ben Trube, Writer
Hi,
Very interesting! How would you go about simulating the chaos game on a computer program, without having to manually do each iteration?
Thanks.
The chaos game is discussed in detail in Chapter 1 of my book Fractals: A Programmer’s Approach, including source code and further expansions of the chaos game. The sample Amazon gives you should get you started but if you want to go deeper, you might find the whole book interesting 🙂
Pingback: 3 Fractals That Show How Beautiful Mathematics Can Be – krisnoble.co.uk